Introduction
If you’ve ever ventured into the world of statistics, chances are you’ve encountered Linear Regression. I remember my first introduction to it, staring at the board and thinking, “What on earth is this bewildering concept?” It felt like an insurmountable puzzle, its purpose and application utterly beyond my grasp. If this echoes your experience, worry not. In this blog, we’re going to demystify Linear Regression together. I’ll guide you through its principles and myriad applications in a way that’s easy to grasp. By the end of this journey, you’ll not only understand Linear Regression but also appreciate its intricate beauty and how it’s applied in solving real-world problems. Let’s embark on this enlightening adventure together, and I promise, the world of Linear Regression will unfold before you in a surprisingly simple and engaging manner.
What is Linear Regression?
Linear Regression is a statistical method used to model the relationship between a dependent variable and one for more independent variables. The goal is to find a linear equation that best fits the data, allowing us to predict the value of the dependent variable based on the values of the independent variables.
Understanding Linear Regression
Dependent Variable(Y): This is what you’re trying to predict or explain. For example, it could be a person’s salary.
Independent Variables (X): These are the factors that you think influence the dependent variable. For instance, years of experience or education level might influence salary.
Linear regression finds the line that best fits the data points available to us. This line is represented by an equation:
$$Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \ldots + \beta_n X_n + \epsilon$$
- Y is the dependent variable we’re trying to predict.
- X1, X2,…, Xn are the independent variables.
- β0 is the intercept, the value of Y when all Xs are 0.
- β1, β2,…, βn are the coefficients, representing the change in Y that the equation doesn’t explain.
- ϵ represents the error term, the part of Y that the equation doesn’t explain.
Why Use Linear Regression?
- Simplicity – It’s a straightforward way to understand relationships between variables.
- Prediction – It allows us to predict the value of a dependent variable based on the values of independent variables.
- Inference – It helps us understand the impact of each independent variable on the dependent variable.
Example of Linear Regression:
Imagine we want to predict a person’s salary based on their years of experience. In this case, the salary is the dependent variable (Y), and the years of experience is the independent variable (X).
- Collect Data: Suppose we collect data on various individuals’ salaries and their years of experience.
- Fit the Linear Model: We use statistical software to find the line that best fits our data. Let’s say we find the equation:
$$ Salary = 30000 + 5000 * Years Of Experience $$- This equation means that the base salary (with 0 years of experience) is $30,000.
- For each additional year of experience, the salary increases by $5,000.
- Make Predictions: With this model, we can now predict the salary of a person with any number of years experience. For example, a person with 10 years of experience would have an estimated salary of $80,000 (calculated as 30000 + 5000 * 10).
Applications of Linear Regression
Linear regression is widely used in predictive modeling, particularly in the fields of finance and economics. By analyzing historical data, linear regression helps in forecasting future trends and outcomes. For example, in finance, it can be utilized to predict stock prices or interest rates based on various economic indicators. Similarly, in economics, it can aid in predicting consumer spending patterns or inflation rates.
In marketing analysis, linear regression is instrumental in understanding the impact of different factors on sales and customer behavior. Marketers can use this technique to assess the influence of variables such as advertising expenditure, pricing strategies, or market demographics on product sales. By employing linear regression, they can gain valuable insights into consumer preferences and market trends, enabling them to make informed decisions regarding their marketing strategies.
- Linear regression aids predictive modeling by forecasting future trends based on historical data.
- In marketing analysis, it helps understand the impact of various factors on sales and customer behavior.
Understanding Data Science with Linear Regression
Statistical Analysis
In the realm of data science, statistical modeling is a fundamental aspect that enables professionals to derive meaningful insights from complex datasets. Linear regression serves as a key statistical tool in this domain, allowing analysts to explore and understand the relationships between different variables within the data. By applying linear regression, data scientists can quantify the impact of one variable on another, thereby facilitating informed decision-making processes. This method of data analysis provides a structured approach to uncovering patterns and trends, ultimately contributing to the development of robust models for predictive purposes.
Data Modeling
Data scientists leverage linear regression to construct intricate models that elucidate and predict real-world phenomena. Through meticulous analysis and interpretation of data, these models offer valuable insights into various scenarios, ranging from economic trends to consumer behavior. By incorporating diverse variables into the model, data scientists can effectively simulate potential outcomes and make informed projections based on historical data patterns. This process of data modeling plays a pivotal role in facilitating evidence-based decision-making across numerous industries, underscoring the significance of linear regression in contemporary data science practices.
Visualizing Linear Regression
Graphical Representation
Data visualization is a crucial aspect of understanding linear regression. By creating visual representations of the relationship between variables, complex data becomes more accessible and comprehensible. Graphs, scatter plots, and trend lines are commonly used to illustrate how one variable impacts another in a linear regression model. These visual aids provide a clear depiction of the direction and strength of the relationship, making it easier for analysts and stakeholders to interpret the findings.
Utilizing graphical representation not only enhances the understanding of linear regression but also facilitates effective communication of insights derived from the data. Visualizations enable data scientists to convey their findings to a broader audience, including non-technical stakeholders, by presenting compelling visuals that highlight the practical implications of their analyses.
Using the example of our Salary Linear Equation above, we visualized the equation:
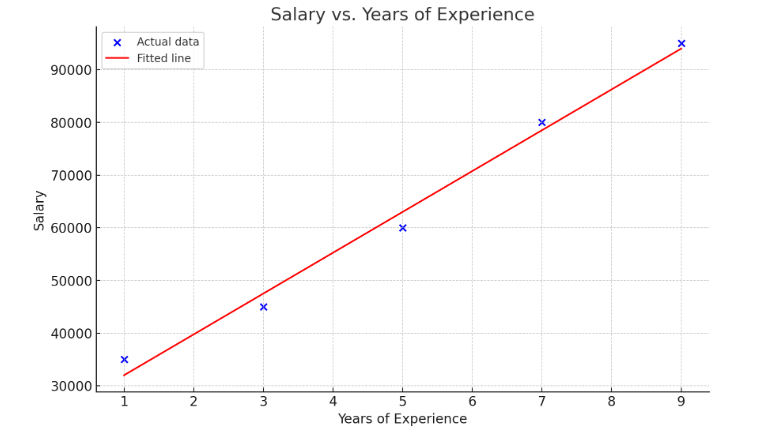
This linear regression model has been applied to the example data, resulting in the following fitted line equation for predicting salary based on years of experience:
$$Salary = 24250 + 7750 * Years Of Experience$$
Here’s how to interpret this model:
- Intercept(β0) = $24,250: This is the starting salary for someone with 0 years of experience.
- Slope(β1) = $7,750: For each additional year of experience, the salary is expected to increase by $7,750.
The plot visualizes the actual data points (in blue) and the linear regression line (in red) that fits these points. This line represents our model’s prediction across different years of experience, illustrating how salary increases with experience according to our linear regression model.
Real-World Examples
In everyday applications, linear regression is employed to solve real-world problems across various industries. For instance, in healthcare, it can be used to predict patient outcomes based on different medical interventions. In manufacturing, linear regression helps optimize production processes by identifying key factors that influence product quality or efficiency. These real-world examples demonstrate the versatility and practical significance of linear regression in addressing complex challenges and making informed decisions.
Unveiling the Power of Linear Regression
Realizing the Potential
Linear regression, through its application of regression analysis, empowers data scientists and analysts to uncover valuable insights from complex datasets. By employing linear modeling, professionals can gain a deeper understanding of the relationships between variables and make informed predictions based on historical trends. This technique not only provides a structured framework for analyzing data but also serves as a cornerstone for developing robust models in various domains. The power of linear regression lies in its ability to distill intricate data into meaningful interpretations, thereby enabling evidence-based decision-making processes.